Lie derivative of forms
Let $X$ be a vector field and $\phi$ its flow. Let $\alpha$ be a $p$-form, we define:
$$ \mathcal { L } _ { X } ( \alpha )=\frac{d}{d t}\left[\phi_{t}^{*} \alpha^{}\right]_{t=0}=\lim _{t \rightarrow 0} \frac{\phi_{t}^{*} \alpha_{\phi_{t} x}-\alpha_{x}}{t} $$in the sense that
$$ \left[\frac{d}{d t} \phi_{t}^{*} \alpha^{}\right]\left(\mathbf{Y}_{1}, \ldots, \mathbf{Y}_{p}\right)= $$ $$ =\frac{d}{d t}\left[\phi_{t}^{*} \alpha^{}\left(\mathbf{Y}_{1}, \dots, \mathbf{Y}_{p}\right)\right]=\frac{d}{d t}|_{t=0}\left\{\alpha^{}\left[\phi_{t *} \mathbf{Y}_{1}, \ldots, \phi_{t *} \mathbf{Y}_{p}\right]\right\} $$More explicitly:
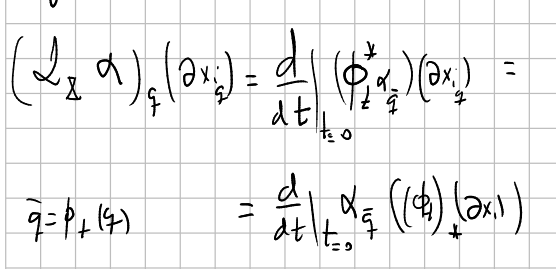
If we define vector fields $Y_i$ extending the previous vectors in a invariant way respect to the flow $\phi$, that is, $Y_i(\phi_t x)=\phi_{t*}Y_i$ then
$$ \mathcal{L}_{\mathbf{X}} \alpha^{}\left(\mathbf{Y}_{1}, \ldots, \mathbf{Y}_{p}\right)=\frac{d}{d t}\left[\alpha_{\phi_{t} x}^{}\left(\mathbf{Y}_{1}, \ldots, \mathbf{Y}_{p}\right)\right]_{t=0} $$That is, the Lie derivative of a $p$-form measure the rate of change along the flow of $X$ of the $p$-form applied to invariant vector fields along $X$.
It can be generalized to Lie derivative for tensors in general.
Useful formulas: formulas for Lie derivative, exterior derivatives, bracket, interior product.
Proposition
A differential $k$-form $\omega$ on $M$ is invariant under the flow of a vector field $X$, i.e.,
$$ \left.\omega\right|_{\exp (\varepsilon X) x}=\exp (-\varepsilon X)^{*}\left(\left.\omega\right|_{x}\right) $$if and only if $\mathcal{L}_X(\omega)=0$
$\blacksquare$
Proof
See @olver86 proposition 1.65.
$\blacksquare$
Especial case: the Lie derivative of a volume form leads to the idea of divergence.
________________________________________
________________________________________
________________________________________
Author of the notes: Antonio J. Pan-Collantes
INDEX: